Erasing Integrated Learning : A Simple yet Effective Approach for Weakly Supervised Object Localization

Oct 1, 2020·
Jinjie Mai
,
Meng Yang
,
Wenfeng Luo
· 6 mins read
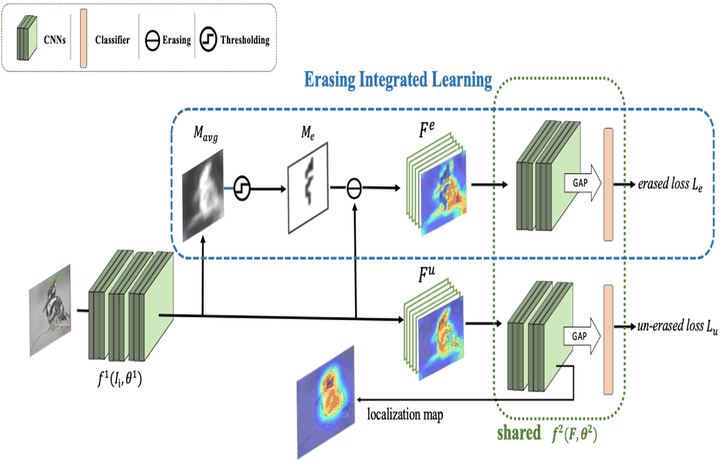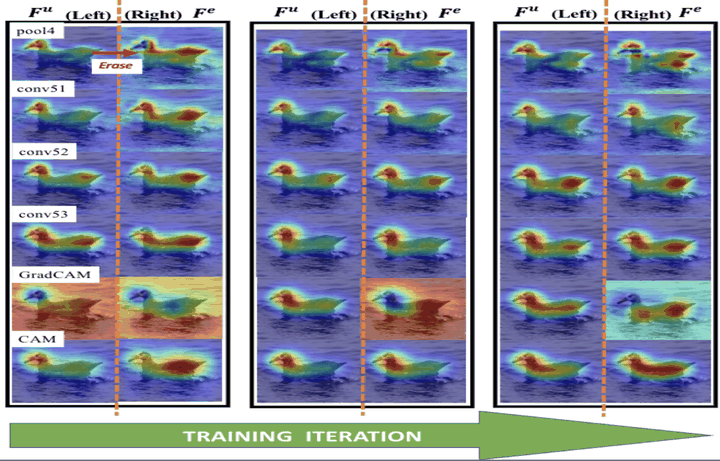When EIL is inserted at a feature map, an average map $M_{avg}$ is first produced by channel-wise average pooling. With thresholding $M_{avg}$ to obtain an erasing mask $M_{e}$, the erased feature map $F^{e}$ by $M_{e}$ and the unerased $F^{u}$ are fed into the network again under a shared dual-branch treatment.
Abstract
Weakly supervised object localization (WSOL) aims to localize object with only weak supervision like image-level labels. However, a long-standing problem for available techniques based on the classification network is that they often result in highlighting the most discriminative parts rather than the entire extent of object. Nevertheless, trying to explore the integral extent of the object could degrade the performance of image classification on the contrary. To remedy this, we propose a simple yet powerful approach by introducing a novel adversarial erasing technique, erasing integrated learning (EIL). By integrating discriminative region mining and adversarial erasing in a single forward-backward propagation in a vanilla CNN, the proposed EIL explores the high response class-specific area and the less discriminative region simultaneously, thus could maintain high performance in classification and jointly discover the full extent of the object. Furthermore, we apply multiple EIL (MEIL) modules at different levels of the network in a sequential manner, which for the first time integrates semantic features of multiple levels and multiple scales through adversarial erasing learning. In particular, the proposed EIL and advanced MEIL both achieve a new state-of-the-art performance in CUB-200-2011 and ILSVRC 2016 benchmark, making significant improvement in localization while advancing high performance in image classification.
Type
Publication
IEEE/CVF Conference on Computer Vision and Pattern Recognition

Formally, we denote the training image set as $I=\{\{I_i,y_i\}\}^N_{i=1}$, where $y_i=\{1,2,...,C\}$ is the label of the image $I_i$, $C$ is total classes of images and $N$ is the amount of images. Let $\theta$, lowercase $f$, and uppercase $F$ denote network parameters, functions, and feature maps, respectively.

The network $f^1(I,\theta^1)$ before EIL is applied can produce the original unerased feature map, which is denoted as $F^{u}\leftarrow f^1(I_i,\theta^1)$ and $F^{u}\in\mathcal{R} ^ {K \times H \times W}$, where $K$ stands for the number of channels, $W$ and $H$ for the width and height, respectively. We make use of $F^{u}$ as self-attention to generate the erasing mask. Specifically, we compress $F^{u}$ into an average map $M_{avg}\in\mathcal{R} ^ {1 \times H \times W}$ through channel-wise average pooling. Then we apply a hard threshold $\gamma$ on $M_{avg}$ to produce the erasing mask $M_e\in\mathcal{R} ^ {1 \times H \times W}$, in which the spatial locations of those pixels having intensity greater than $\gamma$ are set to zero. We perform the erasing operation by doing spatial-wise multiplication between unerased feature map $F^{u}$ and mask $M_{e}$, to produce the erased feature map $F^{e}\in\mathcal{R} ^ {K \times H \times W}$.

Afterwards, both the unerased feature map $F^{u}$ and the erased counterpart $F^{e}$ are fed into the latter part of the network $f^2(F,\theta^2)$ together. As these two data streams are processed by the same function $f^2$ and parameters $\theta^2$, such structure can be regarded as a dual-branch network of shared weights. More specifically, $f^2(F,\theta^2)$ produces class activation maps (CAM) \cite{zhou2016learning}, applies global average pooling \cite{lin2013network} on CAM and utilizes a fully connected layer followed by softmax operation to get the prediction score $p$ for each branch, with $p^{u}$ and $p^{e}$ for the erased and the unerased, respectively. In the end, the classification losses from the two branches will be added up to calculate the total loss $\mathcal{L}$. Note that we also introduce a loss weighting hyperparameter $\sigma$ to control the relative importance between the unerased loss $\mathcal{L}^{u}$ and the erased loss $\mathcal{L}^{e}$.

\begin{algorithm}
    \SetAlgoLined
    \KwInput{Input image $I=\{\{I_i,y_i\}\}^N_{i=1}$ from $C$ classes, erasing threshold $\gamma$, weighting hyperparameter $\sigma$}
    \While {training is not convergent}{
    Calculate the feature map $F^{u}\leftarrow f^1(I_i,\theta^1)$ \;
    Calculate the average map $M_{avg}=\frac{\sum^K_{i=1}F^{u}_i}{K}$\;
    Calculate the erasing mask $M_{e_{i,j}}=\begin{cases}
                                    0, &\quad if\ M_{avg_{i,j}}\ge \gamma\\
                                    1, &\quad else\\
                                \end{cases}$\;
    Get the erased feature map $F^{e}=F^{u}\otimes M_{e}$ \;
    Calculate prediction of $F^{e}$: $p^{e}\leftarrow f^2(F^{e},\theta_2)$ \;
    Calculate prediction of $F^{u}$: $p^{u}\leftarrow f^2(F^{u},\theta_2)$ \;
    Obtain erased loss: $\mathcal{L}_{e}=-\frac{1}{C}\sum_c y_{i,c} log(p^{e}_c)$ \;
    Obtain unerased loss:$\mathcal{L}_{u}=-\frac{1}{C}\sum_c y_{i,c} log(p^{u}_c)$\;
    Calculate the total loss: $\mathcal{L}=\mathcal{L}_{u}+\sigma \mathcal{L}_{e}$ \;
    Back-propagate and update parameters $\theta^1$, $\theta^2$ \;
    }
     \caption{Training algorithm for EIL}
     \label{al:1}
\end{algorithm}
Weakly Supervised Learning Object Localization