TrackNeRF: Bundle Adjusting NeRF from Sparse and Noisy Views via Feature Tracks

Sep 1, 2024·
Jinjie Mai
,
Wenxuan Zhu
,
Sara Rojas
,
Jesus Zarzar
,
Guocheng Qian
,
Abdullah Hamdi
,
Bing Li
,
Silvio Giancola
,
Bernard Ghanem
· 6 mins read
Reconstruction quality v.s. baselines under 35% camera noise from 3 views
Abstract
Neural radiance fields (NeRFs) generally require many images with accurate poses for accurate novel view synthesis, which does not reflect realistic setups where views can be sparse and poses can be noisy. Previous solutions for learning NeRFs with sparse views and noisy poses only consider local geometry consistency with pairs of views. Closely following bundle adjustment in Structure-from-Motion (SfM), we introduce TrackNeRF for more globally consistent geometry reconstruction and more accurate pose optimization. TrackNeRF introduces feature tracks, i.e. connected pixel trajectories across all visible views that correspond to the same 3D points. By enforcing reprojection consistency among feature tracks, TrackNeRF encourages holistic 3D consistency explicitly. Through extensive experiments, TrackNeRF sets a new benchmark in noisy and sparse view reconstruction. In particular, TrackNeRF shows significant improvements over the state-of-the-art BARF and SPARF by ~8 and ~1 in terms of PSNR on DTU under various sparse and noisy view setups. The code is available at https://tracknerf.github.io/.
Type
Publication
European Conference on Computer Vision

Method Overview

Our method addresses the challenge of learning NeRF from sparse and noisy views by enforcing holistic multiview consistency through track-based bundle adjustment. Unlike prior methods that only use local pairwise constraints, we introduce a track-wise loss that aligns feature correspondences across all views.

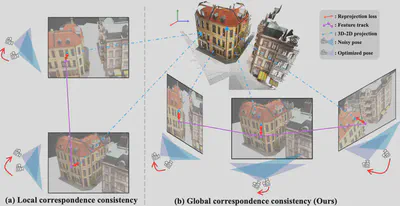
Overview of our TrackNeRF pipeline

Track-Based Bundle Adjustment

Given that all views originate from a single 3D scene, corresponding points across all views should project back to the same 3D landmark. Inspired by bundle adjustment (BA) in Structure-from-Motion, we formulate a track-wise objective that minimizes the reprojection error across all feature correspondences in a track:

\[ E_{BA}=\sum_k \sum_{(\mathbf{u}_i,\mathbf{v}_j)\in \mathcal{T}_{(k)}} \| h (\mathbf{u}_i) - \mathbf{v}_j \| \]

where \((\mathbf{u}_i,\mathbf{v}_j)\) are correspondences inside feature track \(\mathcal{T}_{k}\). The function \(h\) lifts a pixel onto its 3D location and projects it to another view, enforcing holistic consistency across all images.

Track Extraction

Feature tracks are extracted by linking dense correspondences across multiple images. Given a feature matcher, correspondences between image pairs are chained transitively to form continuous tracks, ensuring that every feature track represents a set of 2D points corresponding to the same 3D point:

\[ \mathcal{T}_k = \{\mathbf{u}, \mathbf{v}, \mathbf{q}, ...\} \]

To improve accuracy, we jointly optimize feature correspondences across all views.

Track Keypoint Adjustment

To refine the extracted feature tracks, we optimize keypoint locations by minimizing the feature distance between matched points:

\[ E^k_{TKA}=\sum_{(\mathbf{u}_i,\mathbf{v}_i)\in \mathcal{T}_{(k)}} w_{\mathbf{u}_i\mathbf{v}_j} \| \mathbf{F}(\mathbf{u}_i) - \mathbf{F}(\mathbf{v}_j) \| \]

where \(\mathbf{F}\) extracts pixel-wise features, and \(w_{\mathbf{u}_i\mathbf{v}_j} \) is the matching confidence. This track-wise keypoint adjustment improves multiview consistency and provides more accurate keypoints for NeRF supervision.

Track Reprojection Loss

Previous NeRF methods optimize correspondence at the pairwise level, which can introduce inconsistencies due to local feature extractor noise. To address this, we propose a track reprojection loss that enforces global geometric consistency. This loss minimizes the reprojection error of all correspondences in a feature track, ensuring that all feature points align with the same 3D landmark:

\[ \mathcal{L}_{\text{Track}} = \sum_k \sum_{(\mathbf{u}_i,\mathbf{v}_j)\in \mathcal{T}_k} \frac{1}{| \mathcal{T}_k| } \rho \left( \mathbf{u}_i - \pi \left( \hat{P}_i^{-1} \hat{P}_j \pi^{-1} ( \mathbf{v}_j, \hat{z}(\mathbf{v}_j; \theta, \hat{P}_i) ) \right) \right) \]

where \(\rho\) is the Huber loss function, \(\pi\) is the camera projection function, and \(\pi^{-1}\) is the backprojection operator using the depth \(\hat{z}(\mathbf{v}_j; \theta, \hat{P}_i)\). This loss enforces consistency of all-to-all correspondences in a feature track.

Depth Regularization

To enhance NeRF’s geometry, we introduce depth regularization inspired by monocular depth estimation. This loss encourages depth gradients to align with image gradients:

\[ \mathcal{L}_{\text{Depth}} = \sum_{i,j}^{\Psi} | \nabla_x D^{\Psi}_{ij} | e^{-\| \nabla_x I^{\Psi}_{ij} \| } + | \nabla_y D^{\Psi}_{ij} | e^{-\| \nabla_y I^{\Psi}_{ij} \| } \]

where \(\nabla\) is the vector differential operator, \(D\) is the disparity map (reciprocal of depth), \(I\) is the RGB image, and \(\Psi\) represents sampled image patches. This helps to reduce artifacts such as floaters in NeRF reconstructions.

NeRF Training Objective

Our final objective combines photometric loss, depth regularization, and track reprojection loss:

\[ \mathcal{L} = \mathcal{L}_{\text{Photometric}} + \lambda_{\text{Depth}} \mathcal{L}_{\text{Depth}} + \lambda_{\text{Track}} \mathcal{L}_{\text{Track}} \]

where \(\lambda_{Depth}\) and \(\lambda_{Track}\) control the weighting of the losses. This formulation enables joint optimization of NeRF and multiview feature correspondences, leading to improved consistency and 3D geometry reconstruction from sparse views.

NeRF Bundle Adjustment Feature Tracks